Notebook 25
Derivadas
A definição padrão da derivada, encontrada em qualquer livro de cálculo:
\begin{equation} f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} \end{equation}pode ser diretamente utilizada para o cálculo numérico de derivadas, escolhendo $h$ suficientemente pequeno:
\begin{equation} f'(x) \simeq \frac{f(x+h)-f(x)}{h} \end{equation}Esta implementação é conhecida como a da diferença para frente (forward difference). Obviamente, nada impede que a diferença seja tomada para trás (backward difference):
\begin{equation} f'(x) \simeq \frac{f(x)-f(x-h)}{h} \end{equation}Em geral as duas implementações são essencialmente equivalentes. Em alguns casos, como quando existem descontinuidades na derivada ou em condições de contorno peculiares, pode acontecer de uma funcionar e a outra não.
O método da diferença central (central difference) em geral oferece uma precisão substancialmente maior para o mesmo tamanho do passo $h$, apesar de não utilizar o valor da função no ponto $x$:
\begin{equation} f'(x) \simeq \frac{f(x+h/2)-f(x-h/2)}{h} \end{equation}Esse método requer o conhecimento da função nos pontos $x-h/2$ e $x+h/2$, o que em geral não acontece para dados experimentais amostrados em intervalos regulares. Neste caso, a expressão padrão para o método da diferença central pode ser adaptada para:
\begin{equation} f'(x) \simeq \frac{f(x+h)-f(x-h)}{2h} \end{equation}No caso de valores amostrados, um "mistura" dessas duas últimas fórmulas pode ser interessante. Os pontos na figura abaixo mostram os valores conhecidos da função. Para calcular o valor da derivada em (a) utilizamos a fórmula acima, considerando o intervalo $2h$. Entretanto, é possível calcular o valor da derivada em (b) utilizando a fórmula padrão.

Exercícios
| x | 0,00 | 0,63 | 1,26 | 1,88 | 2,51 | 3,14 | 3,77 | 4,40 | 5,03 | 5,65 | 6,28 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| V | 0,00 | 0,59 | 0,95 | 0,95 | 0,59 | 0,00 | -0,59 | -0,95 | -0,95 | -0,59 | -0,00 |
A tabela e o gráfico abaixo mostram o campo calculado com os diferentes métodos descritos acima. $E_{fw}$, $E_{bw}$ e $E_{ce}$ correspondem aos campos calculados com os métodos das diferenças para frente, para trás e central, respectivamente.
Reproduza a tabela e o gráfico.
| x | 0,00 | 0,63 | 1,26 | 1,88 | 2,51 | 3,14 | 3,77 | 4,40 | 5,03 | 5,65 | 6,28 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Efw | - | -0,94 | -0,58 | -0,00 | 0,58 | 0,94 | 0,94 | 0,58 | 0,00 | -0,58 | -0,94 |
| Ebw | -0,94 | -0,58 | -0,00 | 0,58 | 0,94 | 0,94 | 0,58 | 0,00 | -0,58 | -0,94 | - |
| Ece | - | -0,76 | -0,29 | 0,29 | 0,76 | 0,94 | 0,76 | 0,29 | -0,29 | -0,76 | - |

As linhas que passam pelos pontos não representam um modelo para os dados, mas foram adicionadas somente para guiar os olhos (sem as linhas o gráfico fica muito confuso).
Como os dados foram simulados, sabemos que a derivada usando o método das diferenças centrais é o que melhor aproxima o valor exato do campo. Entretanto, ele não fornece valores para o primeiro e o último ponto onde o potencial foi medido.
O método das diferenças para frente faz com que o campo calculado fique "atrasado" com relação ao calculado exatamente, enquanto o método das diferenças para trás faz com que fique "adiantado". As condições nas fronteiras também ficam diferentes: o método das diferenças para frente não fornece um valor para o extremo direito, enquanto o método das diferenças para trás não fornece um valor para o extremo esquerdo.

Note que para integrar a trajetória é necessário conhecer o valor do campo em pontos arbitrários do espaço. Para obtê-los utilize uma interpolação linear entre os pontos calculados no exercício anterior.

Como em qualquer modelagem numérica, a "qualidade" do resultado depende do que você precisa. Qual o resultado mais confiável?
O gráfico a seguir mostra os mesmos cálculos realizados assumindo 1000 pontos para o potencial e um $dt$ dez vezes maior na integração da trajetória. Com esses parâmetros, parece razoável supor que essa é a trajetória da partícula, pois os três métodos concordam.

Note que, se comparados ao resultado (supostamente) esperado, os parâmetros anteriores fornecem informações potencialmente contraditórias. Se consideramos a posição final, o método das diferenças para frente chega a um resultado mais próximo do esperado do que os demais métodos. Entretando, no meio do caminho o método das diferenças centrais oferece um melhor resultado.
Em resumo: antes de programar o seu problema, estude-o minuciosamente.

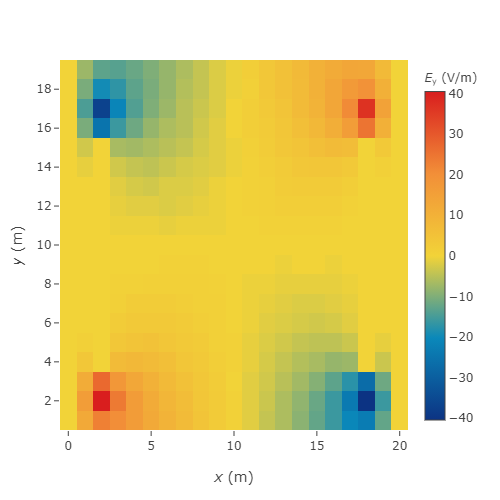
Os gráficos a seguir mostram as componentes $E_x$ e $E_y$ do campo elétrico obtidas utilizando o método das diferenças centrais para calcular o gradiente.
Reproduza as figuras.