

Exercícios sobre gráficos básicos
Um caminhão percorre um pequeno trecho de uma serra sinuosa. Seus ocupantes registram a velocidade do veículo a cada 10 segundos, durante 2 minutos. Os dados estão apresentados na tabela a seguir.
| t (s) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| v (m/s) | 9,0 | 7,2 | 4,4 | 3,6 | 3,1 | 1,9 | 2,8 | 6,3 | 8,3 | 7,4 | 6,3 | 5,8 | 3,7 |
Faça um gráfico da velocidade em função do tempo.
Utilizando os dados do item anterior e considerando que a primeira medida foi feita no km 27 da rodovia e que a velocidade medida no início do intervalo representa a velocidade média do intervalo, faça um gráfico da posição em função do tempo.
Utilizando os dados do item anterior e considerando que a primeira medida foi feita no km 27 da rodovia e que a velocidade média no intervalo é a média das velocidades medidas no início e no fim do intervalo, faça um gráfico da posição em função do tempo, superpondo-o ao gráfico obtido para o item anterior.
Faça um gráfico da chamada curva deltoide, que é definida parametricamente pelas equações:
onde $0\le\theta\lt2\pi$. Escolha um conjunto de valores para $\theta$ entre $0$ e $2\pi$ e calcule $x$ e $y$ para cada um deles utilizando as equações acima e então faça o gráfico de $y$ em função de $x$. Você deve obter algo parecido com a figura abaixo:

Utilzando essa metodologia podemos fazer um gráfico polar $r = f(\theta)$ para uma função $f$ calculando $r$ para um intervalo de valores de $\theta$ e então convertendo $r$ e $\theta$ para coordenadas cartesianas utilizando as equações usuais $x = r\cos\theta$ e $y = r\sin\theta$. Utilize esse método para fazer um gráfico da espiral galileana $r = \theta^{\,2}$ para $0\le\theta\le10\pi$. Você deve obter uma figura como a que segue:
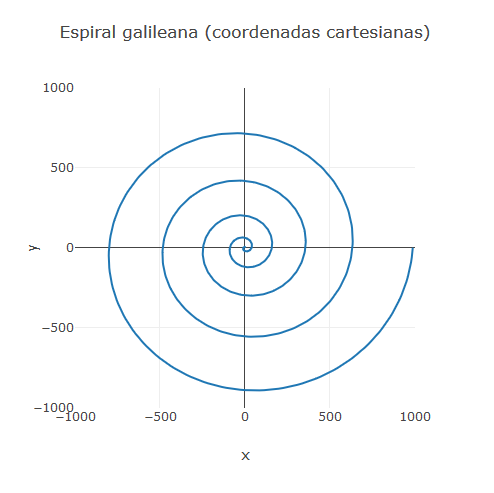
Estude o Plotly.js (ou o aplicativo de sua preferência) e veja como produzir o mesmo gráfico em coordenadas polares, de modo a obter uma figura como a que segue:
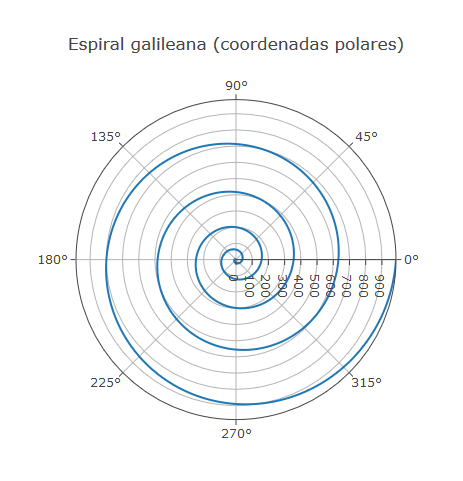
Utilizando o mesmo método, faça um gráfico da função de Fey:
no intervalo $0\le\theta\le24\pi$.