Este documento explora uma simulação sobre conservação da energia mecânica disponível no site oPhysics: Interactive Physics Simulations. Sugerimos fortemente um "passeio" por todo o site, que traz mais de 100 interessantes simulações desenvolvidas por Tom Walsh, um veterano professor de física, na plataforma GeoGebra.

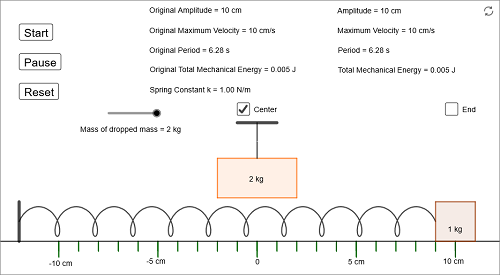
A simulação consiste em uma massa que oscila ligada a uma mola de constante elástica. Em um determinado instante, uma segunda massa é adicionada à massa original do oscilador. O usuário pode escolher dois parâmetros: (a) o valor da massa adicionada, com 4 possibilidades e (b) o ponto em que a adição é realizada, com duas possibilidades (no ponto de equilíbrio ou no ponto de deslocamento máximo). A simulação calcula e mostra para o usuário os valores das amplitudes, velocidades máximas, períodos e energias mecânicas totais antes e depois da adição da segunda massa.

Acesse a simulação e faça os "experimentos" para preencher as tabelas abaixo. Em caso de acerto, as células ficarão verdes, em caso de erro, vermelhas. Digite os números com no máximo dois algarismos significativos (por exemplo, se 0,3333 digite 0,33, se 0,006667, digite 0,0067).

Teste sua interpretação do que aconteceu nos "experimentos" respondendo às questões que seguem. No final, você poderá ver quantas questões acertou na primeira tentativa.

Antes de começar, esboce alguns gráficos para ganhar uma visão mais abrangente do que está acontecendo. Para cada posição de adição de massa (no ponto de equilíbrio ou no ponto de amplitude máxima), faça esboços de gráfico para:

Fundamentação teórica

Adição da massa no ponto de equilíbrio

Conservação do momento linear

O momento linear do sistema é conservado no momento da adição da massa:

\begin{eqnarray} p_i & = & M v_M \\ p_f & = & (M+m) v_{Mm} \\ p_i & = & p_f \\ v_{Mm} & = & \frac{M}{M+m} v_{M} \\ \end{eqnarray}

Conservação da energia

A energia mecânica total não é conservada no momento da adição da massa:

\begin{eqnarray} E_i & = & \frac{1}{2} M v_M^2\\ E_f & = & \frac{1}{2} (M+m) v_{Mm}^2 \\ E_f & = & \frac{1}{2} (M+m) \left( \frac{M}{M+m} \right)^2 v_{M}^2 \\ E_f & = & \frac{M}{M+m} \left( \frac{1}{2} M v_{M}^2 \right) \\ E_f & = & \frac{M}{M+m} E_i \\ \Delta E & = & \frac{E_f-E_i}{E_i}= -\frac{m}{M+m} \\ \end{eqnarray}

Igualando a energia cinética máxima com a energia potencial máxima, obtemos a velocidade após a colisão:

\begin{eqnarray} E_i & = & \frac{1}{2} M v_M^2 = \frac{1}{2} k A_M^2 \\ v_M & = & A_M \sqrt{\frac{k}{M}} \\ E_f & = & \frac{1}{2} (M+m) v_{Mm}^2 = \frac{1}{2} k A_{Mm}^2 \\ v_{Mm} & = & A_{Mm} \sqrt{\frac{k}{M+m}} = A_{Mm} \omega_{Mm} \\ \end{eqnarray}

A relação entre as amplitudes antes e depois da adição da massa é dada por:

\begin{eqnarray} E_f = \frac{1}{2} k A_{Mm}^2 & = & \frac{M}{M+m} E_i = \frac{M}{M+m} \left( \frac{1}{2} k A_{M}^2 \right) \\ A_{Mm} & = & \sqrt{\frac{M}{M+m}} A_M \\ \end{eqnarray}

Equações para as grandezas cinemáticas:

\begin{eqnarray} x_M(t) & = & A_M \cos(\omega_M t) \\ v_M(t) & = & \frac{dx_M}{dt} = - A_M \omega_M \sin(\omega_M t) \\ a_M(t) & = & \frac{d^2x_M}{dt^2} = - A_M \omega_M^2 \cos(\omega_M t) \\ \end{eqnarray} \begin{eqnarray} x_{Mm}(t) & = & A_{Mm} \cos(\omega_M t) \\ v_{Mm}(t) & = & \frac{dx_{Mm}}{dt} = - A_{Mm} \omega_{Mm} \sin(\omega_{Mm} t) \\ a_{Mm}(t) & = & \frac{d^2 x_{Mm}}{dt^2} = - A_{Mm} \omega_{Mm}^2 \cos(\omega_{Mm} t) \\ \end{eqnarray}

Adição da massa no ponto de amplitude máxima

Conservação do momento linear

A conservação do momento no momento da adição da massa não ajuda muito pois:

\begin{equation} p_i = p_f = 0 \\ \end{equation}

Conservação da energia

A energia total é conservada pois no momento da adição da massa toda a energia mecânica está na mola, e a adição da massa não altera o seu comprimento, e portanto, não altera energia a energia no sistema.

Igualando a energia cinética máxima com a energia potencial máxima, obtemos a velocidade após a colisão (neste caso $A_M = A_{Mm}$):

\begin{eqnarray} E_i & = & \frac{1}{2} M v_M^2 = \frac{1}{2} k A_M^2 \\ v_M & = & A_M \sqrt{\frac{k}{M}} \\ E_f & = & \frac{1}{2} (M+m) v_{Mm}^2 = \frac{1}{2} k A_{M}^2 \\ v_{Mm} & = & A_{M} \sqrt{\frac{k}{M+m}} \\ \end{eqnarray}

Equações para as grandezas cinemáticas:

\begin{eqnarray} x_M(t) & = & A_M \cos(\omega_M t) \\ v_M(t) & = & \frac{dx_M}{dt} = - A_M \omega_M \sin(\omega_M t) \\ a_M(t) & = & \frac{d^2x_M}{dt^2} = - A_M \omega_M^2 \cos(\omega_M t) \\ \end{eqnarray} \begin{eqnarray} x_{Mm}(t) & = & A_{M} \cos(\omega_M t) \\ v_{Mm}(t) & = & \frac{dx_{Mm}}{dt} = - A_{M} \omega_{Mm} \sin(\omega_{Mm} t) \\ a_{Mm}(t) & = & \frac{d^2 x_{Mm}}{dt^2} = - A_{M} \omega_{Mm}^2 \cos(\omega_{Mm} t) \\ \end{eqnarray}

Configuração inicial
$M$ (kg)
$k$ (N/m)
$A_i$ (cm)
$v_i$ (cm/s)
$T_i$ (s)
$E_i$ (J)

Adição da massa no ponto de equilíbrio
$m_c$ (kg)
$A_c$ (cm)
$v_c$ (cm)
$T_c$ (s)
$E_c$ (J)

Adição da massa no ponto extremo
$m_e$ (kg)
$A_e$ (cm)
$v_e$ (cm)
$T_e$ (s)
$E_e$ (J)