plotly-logomark

Notebook 30
Ajuste de retas (mínimos quadrados, regressão linear)

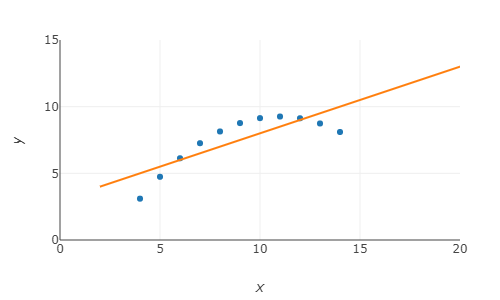
A tabela e o gráfico a seguir mostram valores medidos para a variável $y$ (posição, por exemplo) em função da variável $x$ (tempo, por exemplo). O gráfico também mostra a "melhor reta" ajustada aos dados de acordo com o método exposto a seguir.

$x$	0,5	1,5	2,5	3,5
$y$	0,8	2,1	5,6	6,4

Uma reta é definida pelo seus coeficientes linear $A$ e angular $B$ segundo a equação:

y = A + B x

O método dos mínimos quadrados busca encontrar os valores de $A$ e $B$ que minimizam $Q$ :

Q = \sum_{i} (y_{i} - y (x_{i}))^{2}

onde $(x_{i}, y_{i})$ são as coordenadas do ponto conhecido e $y (x_{i}) = A + B x_{i}$ ao valor da função para $x_{i}$ , de modo que:

Q = \sum_{i} (y_{i} - A - B x_{i})^{2}

O valor de $Q$ será mínimo quando as suas derivadas parciais em relação a $A$ e a $B$ forem simultaneamente iguais a zero:

\begin{array}{rcl} \frac{\partial Q}{\partial A} & = & \sum_{i} y_{i} - A - B x_{i} = 0 \\ \frac{\partial Q}{\partial B} & = & \sum_{i} (y_{i} - A - B x_{i}) x_{i} = 0 \end{array}

ou, equivalentemente:

\begin{array}{rcl} \sum_{i} y_{i} & = & A N + B \sum_{i} x_{i} \\ \sum_{i} x_{i} y_{i} & = & A \sum_{i} x_{i} + B \sum_{i} x_{i}^{2} \end{array}

Os somatórios dependem apenas das coordenadas dos pontos e resultam em quantias (números) bem definidas:

s_{x} = \sum_{i} x_{i}, s_{y} = \sum_{i} y_{i}, s_{x y} = \sum_{i} x_{i} y_{i}, s_{x^{2}} = \sum_{i} x_{i}^{2}

de modo que:

\begin{array}{rcl} s_{y} & = & A N + B s_{x} \\ s_{x y} & = & A s_{x} + B s_{x^{2}} \end{array}

e, finalmente:

\begin{array}{rcl} A & = & \frac{s_{y} s_{x^{2}} - s_{x} s_{x y}}{N s_{x^{2}} - (s_{x})^{2}} \\ B & = & \frac{N s_{x y} - s_{x} s_{y}}{N s_{x^{2}} - (s_{x})^{2}} \end{array}

Exercícios

Examine o código fonte do documento e modifique-o de modo que imprima os valores de $s_{x}$ , $s_{y}$ , $s_{x y}$ , $s_{x^{2}}$ , $A$ e $B$ (8,0, 14,9, 40,0, 21,0, −0,34 e 2,03, respectivamente).
Examine o código fonte do documento e modifique-o de modo que imprima os valores dos pontos extremos da reta ajustada e para $x$ = 1,0, $x$ = 2,0 e $x$ = 3,0 ((0,5, 0,7), (3,5, 6,8), (1,0, 1,7), (2,0, 3,7) e (3,0, 5,8), respectivamente).
Se: $y = A + B x$
então:
$x = - \frac{A}{B} + \frac{1}{B} y = A^{'} + B^{'} y$
de modo que em uma situação ideal:
$B^{'} = \frac{1}{B} \to B B^{'} = 1$
Isso significa que, em princípio, quanto mais próxima da unidade for a grandeza $R = \sqrt{B B^{'}}$ , melhor a reta encontrada descreve os dados. $R$ também pode ser escrito em termos dos somatórios:
$R = \frac{N s_{x y} - s_{x} s_{y}}{\sqrt{(N s_{x^{2}} - (s_{x})^{2}) (N s_{y^{2}} - (s_{y})^{2})}}$
Faça um programa que encontre o valor de $R$ para o conjunto de dados fornecido (0,971).
Considere a equação para uma grandeza $y$ que varia exponencialmente com $x$ : $y = A e^{B x}$
Aplicando o logaritmo obtemos:
$\ln y = \ln A + B x$
Comparando essa equação à equação de uma reta vemos que se fazemos:
$\begin{array}{rcl} y^{'} & \to & \ln y \\ A^{'} & \to & \ln A \\ B^{'} & \to & B \\ x^{'} & \to & x \\ y^{'} & = & A^{'} + B^{'} x^{'} \end{array}$
e obtemos:
$\begin{array}{rcl} A & = & e^{A^{'}} \\ B & = & B^{'} \end{array}$
Modifique o programa de modo que suponha que os dados obedecem uma relação exponencial $y = A e^{B x}$ e determine os valores de $A$ , $B$ e $R$ (0,66, 0,72 e 0,962, respectivamente) e faça o gráfico lin-log.
Considere a equação para uma grandeza $y$ que é proporcional a uma potência de $x$ : $y = A x^{B}$
Aplicando o logaritmo obtemos:
$\ln y = \ln A + B \ln x$
Comparando essa equação à equação de uma reta vemos que se fazemos:
$\begin{array}{rcl} y^{'} & \to & \ln y \\ A^{'} & \to & \ln A \\ B^{'} & \to & B \\ x^{'} & \to & \ln x \\ y^{'} & = & A^{'} + B^{'} x^{'} \end{array}$
e obtemos:
$\begin{array}{rcl} A & = & e^{A^{'}} \\ B & = & B^{'} \end{array}$
Modifique o programa de modo que suponha que os dados obedecem uma relação exponencial $y = A x^{B}$ e determine os valores de $A$ , $B$ e $R$ (1,64, 1,12 e 0.984, respectivamente) e faça o gráfico log-log.
A partir desses resultados, qual das funções (linear, exponencial e potência) melhor descreve os dados?

As tabelas abaixo contêm os dados do que é conhecido como o quarteto de Anscombe.

x	y
10,0	8,0
8,0	7,0
13,0	7,6
9,0	8,8
11,0	8,3
14,0	10,0
6,0	7,2
4,0	4,3
12,0	10,8
7,0	4,8
5,0	5,7

x	y
10,0	9,1
8,0	8,1
13,0	8,7
9,0	8,8
11,0	9,3
14,0	8,1
6,0	6,1
4,0	3,1
12,0	9,1
7,0	7,3
5,0	4,7

x	y
10,0	7,5
8,0	6,8
13,0	12,7
9,0	7,1
11,0	7,8
14,0	8,8
6,0	6,1
4,0	5,4
12,0	8,2
7,0	6,4
5,0	5,7

x	y
8,0	6,6
8,0	5,8
8,0	7,7
8,0	8,8
8,0	8,5
8,0	7,0
8,0	5,3
19,0	12,5
8,0	5,6
8,0	7,9
8,0	6,9

Os quatro conjuntos têm valores essencialmente iguais para todos os descritores estatísticos (valor médio de x, valor médio de y, variância em x, variância em y, correlação entre x e y, coeficientes linear e angular da reta ajustada por mínimos quadrados e valor de R).

Entretanto, constituem distribuições completamente diferentes. O conjunto de dados foi criado por Francis Anscombe em 1973 [ref] para mostrar que a utilização de descritores estatísticos pode levar a erros grosseiros, e que a elaboração e análise de gráficos é essencial para a realização de análises estatísticas adequadas.

Faça os gráficos dos quatro conjuntos de dados e da melhor reta ajustada aos dados utilizando o método dos mínimos quadrados.