Notebook 29
Raízes de funções

Encontrar a(s) raíz(es) de uma função $f(x)$ é encontrar os valores de $x$ para os quais $f(x) = 0$. É o que fazemos frequentemente quando utilizamos a equação quadrática para encontrar as raízes (reais ou imaginárias) de uma equação de segundo grau ($f(x) = ax^2 + bx + c$).

Equivalentemente, é o que precisamos fazer para encontrar os pontos em que duas funções $f(x)$ e $g(x)$ têm o mesmo valor, pois podemos definir uma função $h(x) = f(x) - g(x)$ e buscar as raízes de $h(x)$. Os valores encontrados não serão raízes de $f(x)$ e $g(x)$, mas os valores para os quais $f(x) = g(x)$.

Às vezes é possível encontrar as raízes de uma função analiticamente, mas em geral isso não é possível. Considere, por exemplo, as funções $f(x) = x^2$ e $g(x) = e^{-x}$. Como encontrar o ponto em que são iguais? Encontrando numericamente a raiz da função $h(x) = x^2 - e^{-x}$.

Uma possibilidade é utilizar o "método gráfico", que implica em fazer um gráfico das duas funções sobre o mesmo "papel" e estimar onde as duas se encontram, como na figura a seguir, da qual se pode estimar que $0{,}70 \lt x \lt 0{,}71$.

Frequentemente, entretanto, desejamos uma ferramenta mais "automatizada" para fazer esse serviço, e alguns métodos numéricos vêm a calhar. São muitos os métodos (bissecção, regula false, interpolação, secante, Newton-Raphson, Steffensen, Brent, Ridders...), cada um com suas especificidades e eficiência. No que segue apresentamos o método da bissecção, provavelmente o mais intuitivo e simples de implementar e é mais do que suficiente para situações que não exigem alta performance.

O método da bissecção pode ser usado para encontrar as raízes de uma função contínua $f(x)$ no intervalo $[a,b]$, dado que $f(a)$ e $f(b)$ tenham sinais opostos, ou seja $f(a) \cdot f(b) < 0$. Nestas condições, o teorema do valor intermediário garante a existência de uma raiz no intervalo $[a,b]$.

O método consiste em dividir o intervalo no seu ponto médio $c=\frac{(a+b)}{2}$, e então verificar em qual dos dois subintervalos garante-se a existência de uma raiz. Para tanto, basta verificar se $f(a) \cdot f(c) \lt 0$. Caso afirmativo, existe pelo menos uma raiz no intervalo [a,c]; caso contrário garante-se a existência de uma raiz no intervalo [c,b]. O procedimento é, então, repetido para o subintervalo correspondente à raiz até que $c$ aproxime a raiz com a precisão desejada.

A figura a seguir ilustra o processo. A busca começa fornecendo os valores de $a_1 = 1$ e $b_1 = 2$. Na primeira interação $f((a_1 + b_1)/2) \gt 0$, levando a um novo limite $a_2 = (a_1 + b_1)/2 \gt 0$ para o lado esquerdo. Na segunda interação $f((a_2 + b_1)/2) \lt 0$, levando a um novo limite $b_2 = (a_2 + b_1)/2$ para o lado direito. Na terceira interação $f((a_2 + b_2)/2) \lt 0$, levando a um novo limite $b_3 = (a_2 + b_2)/2$ para o lado direito. Na quarta (e última) interação, $f((a_2 + b_3)/2) \gt 0$, levando a um novo limite $a_3 = (a_2 + b_3)/2$ para o lado esquerdo, já bem próximo da raiz da função. As barras horizontais pretas sobre o gráfico indicam os sucessivos intervalos da operação.

É possível demonstrar que o número máximo $n$ de iterações necessárias para que a aproximação fornecida pelo método estivesse dentro de uma determinada margem de erro (ou tolerância) $\epsilon$ é dado por:

Note que a forma da expressão mais à direita independe da base utilizada para o cálculo do logaritmo.

Exercícios

1. Implemente o método da bissecção para encontrar o ponto de interseção das funções $f(x) = x^2$ e $g(x) = e^{-x}$ com uma precisão da ordem de $10^{-6}$. Quantas interações são necessárias partindo-se do intervalo $a = 0$ e $b = 1$ (19)? Quantas interações são necessárias partindo-se do intervalo $a = 0{,}6$ e $b = 0{,}8$ (17)?
2. Implemente o método da bissecção para encontrar a raiz da função $f(x) = \cos{x}*x$ com uma precisão da ordem de $10^{-6}$. Quantas interações são necessárias partindo-se do intervalo $a = 1$ e $b = 2$ (19)? Quantas interações são necessárias partindo-se do intervalo $a = 1{,}5$ e $b = 1{,}6$ (15)? Note que essa raiz pode ser obtida analiticamente ($x$ = $\pi/2$ = 1,5707963...).
3. Um poço de potencial quadrado finito simétrico em torno da origem é dado por: $$ V(x) = \begin{cases} V_0, & \text{para $x \lt -a$} \\ 0, & \text{para $-a \lt x \lt a$} \\ V_0, & \text{para $x \gt a$} \\ \end{cases} $$

   Tal poço está esquematizado na figura abaixo, onde também está indicada a energia $E$ de uma partícula "presa" nele, dado que $E \lt V_0$.

   

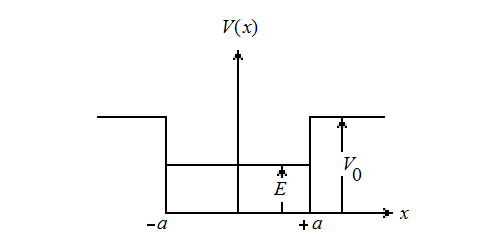
   Fisicamente essa idealização matemática pode ser aproximada, por exemplo, pelo sistema representado na figura abaixo. Nela, um recipiente em vácuo contém uma carga elétrica negativa e um conjunto de eletrodos. Os eletrodos "A" estão aterrados, e portanto o potencial elétrico entre eles é zero (a parte central do poço). Os eletrodos "B" estão a um mesmo potencial negativo, e portanto ambos repelem a carga negativa dentro do poço.

   Classicamente, se a carga tiver uma energia $E \lt V_0$ fica aprisionada entre os eletrodos "B", indo de um lado para o outro. O poço quadrado finito definido acima acontece no para o limite em que a distâncias entre os eletrodos "A" e "B" de cada lado do recipiente tende a zero (as paredes verticais do poço de potencial).

   

   Na abordagem quântica, a função de onda para a carga é solução da equação de Schroedinger independente do tempo em uma dimensão:

   $$ -\frac{\hbar^2}{2m} \frac{\partial^2\psi(x)}{\partial x^2} + V(x) \psi(x) = E \psi(x) $$

   Neste caso, a partícula não pode ter qualquer energia, mas apenas alguns valores quantizados $E_n$ dados pela solução das equações:

   $$ \begin{eqnarray} \tan(k_na) & = & \alpha_n/k_n, & \text{ $n$ ímpar} \\ -\cot(k_na) & = & \alpha_n/k_n, & \text{ $n$ par} \\ \end{eqnarray} $$

   onde $k_n = \sqrt{2mE_n}/\hbar$ e $\alpha_n = \sqrt{2m(V_0 - E_n)}/\hbar$ para $E_n \le V_0$. Explicitando em termos de $E_n$ essas equações ficam:

   $$ \begin{eqnarray} \tan(\frac{\sqrt{2mE_n}}{\hbar}a) & - & \sqrt{\frac{V_0-E_n}{E_n}} & = & 0, \;\;\;\text{ $n$ ímpar} \\ -\cot(\frac{\sqrt{2mE_n}}{\hbar}a) & - & \sqrt{\frac{V_0-E_n}{E_n}} & = & 0, \;\;\;\text{ $n$ par} \\ \end{eqnarray} $$

   Para resolver o problema numericamente, precisamos concretizá-lo, escolhendo valores para as grandezas pertinentes, por exemplo considerando um elétron de massa m = 9,11 × 10⁻³¹ kg em um poço quadrado finito de largura 2a = 1 × 10⁻⁹ m (1 nm) e profundidade V₀ = 6,4 × 10⁻¹⁹ J (4 eV). Neste caso, existem 4 estados ligados, como mostra o gráfico a seguir:

   

   Utilize o método da bisseção para encontrar os níveis de energia permitidos para o poço de potencial descrito acima: