Notebook 24
Transformada discreta de Fourier

O script desse documento implementa o cálculo da DFT (de discrete Fourier transform), que não é tão eficiente quanto a FFT (de fast Fourier transform), mas é bem mais fácil de entender, pois é uma implementação direta da definição da transformada discreta:

\begin{eqnarray} \text{Re}\{g_j\} & = & \frac{1}{\sqrt{N}} \underset{k=0}{\overset{N-1}{\LARGE\Sigma}} \left( \cos\frac{2\pi j k}{N} \text{Re}\{f_k\} + \sin\frac{2\pi j k}{N} \text{Im}\{f_k\} \right) \\ \text{Im}\{g_j\} & = & \frac{1}{\sqrt{N}} \underset{k=0}{\overset{N-1}{\LARGE\Sigma}} \left( \cos\frac{2\pi j k}{N} \text{Im}\{f_k\} - \sin\frac{2\pi j k}{N} \text{Re}\{f_k\} \right) \\ \end{eqnarray}

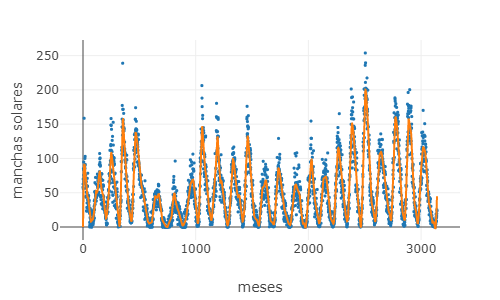
O documento também inclui um arquivo (manchas-solares.js) que contém a quantidade de manchas solares medidas para cada mês ao longo de mais de 260 anos (os dados foram extraídos do excelente livro de Mark Newman Computacional Physcis, que pode ser parcialmente acessado gratuitamente em seu site), mostrados no gráfico a seguir.

O script aplica a transformada discreta de Fourier nesses dados, obtendo os seguintes resultados (explore a ferramenta de zoom para apreciar melhor o gráfico):

O gráfico que segue mostra uma ampliação da região próxima à origem. É possível ver que as componentes real e imaginária da transformada têm um máximo em torno do canal 25.

As frequências dominantes aparecem mais claramente quando fazemos o gráfico do módulo da transformada (a raiz quadrada da soma dos quadrados das partes real e imaginária):

Exercícios

  1. Modifique o script de modo a eliminar das matrizes associadas aos dados transformados as frequências maiores do que 100 e faça a transformada inversa, obtendo a curva filtrada mostrada no gráfico a seguir.

  2. No exercício anterior foi aplicado um "filtro" que removeu as frequências mais altas. Modifique o script de modo que aplique um filtro que remova as baixas frequências, deixando apenas as maiores que 100, obtendo a curva filtrada mostrada no gráfico a seguir.

  3. Faça um programa que simule um sinal harmônico acima de um nível de base e sujeito a um ruído branco (algo como $f(t) = a + b \cos(2 \pi f t) + c \text{ rand}(t)$, onde $a$, $b$, $c$ e $f$ são constantes arbitrárias e $\text{rand}(t)$ é uma função que retorna números aleatórios entre $-1$ e $1$). O gráfico a seguir mostra o resultado para $a$ = 1, $b$ = 0,5 e $c$ = 2 (fica a seu critério encontrar o valor de $f$).

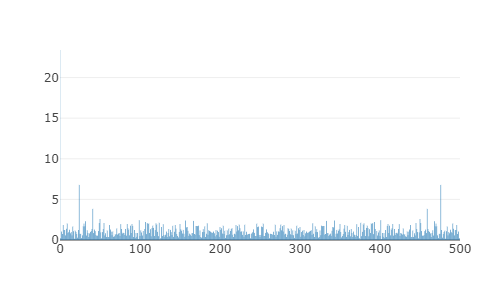
    Obtenha a transformada de Fourier do sinal e faça o gráfico do seu módulo (a raiz quadrada da soma dos quadrados dos termos real e imaginário). Note que além de um "pico" em $f$ = 0 (nível de base), o espectro mostra dois outros "picos" em $f$ = 24 e $f$ = 476, cuja amplitude é maior que 4.

    Aplique um "filtro" que remova o nível de base e o ruído branco.

  4. Em certos contextos a transformada de Fourier pode ser utilizada para compactação de dados sem perda significativa de informação. O gráfico a seguir mostra o trecho de um sinal de um eletrocardiógrafo, composto de 800 pontos (800 números).

    A transformada de Fourier do sinal indica que não há muita informação relevante acima do 40o. canal. Além disso, como trata-se da transformada de um sinal real "puro", a distribuição é, em princípio, simétrica. O gráfico a seguir mostra a amplitude (raiz quadrada da soma dos quadrados das partes real e imaginária) dos canais da transformada.

    Se utilizamos a informação contida nos primeiros 40 canais da distribuição para fazer a transformada inversa obtemos o gráfico abaixo.

    Note que a diferença entre o sinal original e o sinal reconstruído é relativamente pequena e, dependendo da aplicação, irrelevante. Entretanto, ao invés dos 800 números associados à informação original, temos 80 números (40 para a parte real e 40 para a parte imaginária da transformada), representando uma substancial economia no eventual armazenamento ou transmissão dos dados.

    Faça um programa que reproduza as duas últimas figuras acima.