Notebook 20
Equação de Poisson, relaxação, tabelas, Plotly

A lei de Gauss estabelece que o divergente do campo elétrico é proporcional à densidade de cargas:

$$ \nabla \cdot \mathbf{E} = \frac{1}{\epsilon} \rho $$

O campo elétrico, por sua vez, pode ser escrito como o negativo do gradiente do potencial elétrico:

$$ \mathbf{E} = -\nabla \phi $$

Juntando as duas equações, obtemos a equação de Poisson:

$$ \nabla^2 \phi = - \frac{1}{\epsilon} \rho $$

Em duas dimensões essa equação pode ser escrita, em coordenadas cartesianas, como:

$$ \left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} \right) \phi(x,y) = - \frac{1}{\epsilon} \rho(x,y) $$

Se $\phi$ é uma função real suave de números reais, sua derivada segunda pode ser aproximada por:

$$ {\frac {d^{2}\varphi (x)}{{dx}^{2}}}={\frac {\varphi (x{-}h)-2\varphi (x)+\varphi (x{+}h)}{h^{2}}}\,+\,{\mathcal {O}}(h^{2})\ $$

Em duas dimensões, e resolvendo para $\phi(x,y)$, a aproximação leva a:

\begin{eqnarray} \phi (x,y) & = & {\tfrac {1}{4}}\left(\phi (x{+}h,y)+\phi (x,y{+}h)+\phi (x{-}h,y)+\phi (x,y{-}h)\,-\,h^{2}{\nabla }^{2}\phi (x,y)\right) \\ & \, & + \,{\mathcal {O}}(h^{4}) \\ \end{eqnarray}

Considerando, como visto acima, que:

$$ \nabla^2 \phi(x,y) = - \frac{1}{\epsilon} \rho(x,y) $$

e que numericamente um novo valor $\phi^*(x,y)$, em uma rede de espaçamento $h$, pode ser repetidamente calculado até atingir um critério arbitrário de convergência a partir dos valores de $\phi$ dos seus vizinhos, obtemos:

$$ \phi^*(x,y)={\tfrac {1}{4}}\left(\phi (x{+}h,y)+\phi (x,y{+}h)+\phi (x{-}h,y)+\phi (x,y{-}h)\,+\,h^{2}\frac{1}{\epsilon} \rho(x,y)\right) $$

Considere uma região superficial plana onde são colocados alguns eletrodos ligados a baterias que lhes atribuem diferentes potenciais elétricos. A figura abaixo esquematiza esta situação para uma região quadrada com o perímetro "aterrado" e com quatro eletrodos em seu interior, dois a 100 V e dois a −100 V.

O problema é calcular o valor do potencial elétrico nos outros pontos da superfície (aqueles marcados com um "0"). O algoritmo é mais ou menos o seguinte:

Crie uma matriz bidimensional A cujos elementos a_i,j contém os valores dos potenciais iniciais em cada célula, como na figura.
Crie uma matriz similar B e atribua a cada elemento desta nova matriz o valor da média dos vizinhos mais próximos utilizando a matriz A, ou b_i,j = (1/4) × (a_i-1,j + a_i,j+1 + a_i+1,j + a_i,j-1).
Calcule a diferença entre as duas matrizes, elemento a elemento e guarde a maior delas, m = max(|a_i,j − b_i,j|). Se este número for maior que a tolerância t (precisão) desejada, ou m>t, guarde a matriz B no lugar da A e repita o procedimento; se não, pare os cálculos.

Dois cuidados são necessários:

Como as células das bordas não têm alguns dos vizinhos, elas devem ser mantidas sempre fixas.
É preciso ter uma estratégia para saber que células podem ser modificadas ou não. Uma solução seria criar uma outra matriz C similar às outras e colocar 0 nas células que podem ser variadas e números diferentes de 0 nas demais. Esta matriz nunca muda e fica de referência durante os cálculos.

A figura a seguir mostra o resultado para uma tolerância de 0,1 V, o que requer cerca de 50 interações.

Exercícios

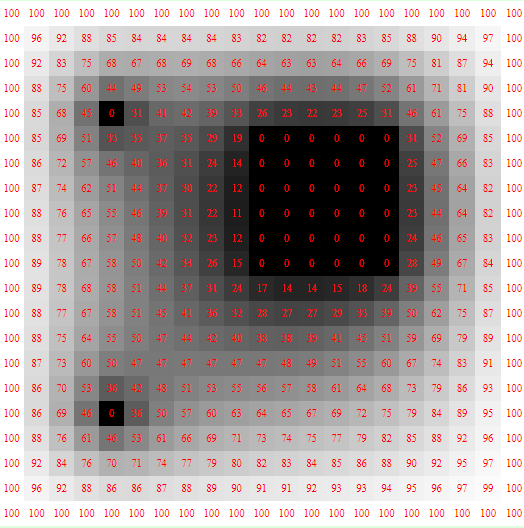
Modifique o script para produzir um sistema cujo perímetro está a um potencial específico e que contém uma região interna "aterrada" (0 V) e calcule os potenciais nos outros pontos da rede, como no exemplo abaixo. Note que no interior da região aterrada o potencial é o mesmo em todos os pontos, como era de se espera devido ao efeito de "blindagem".
No exemplo deste documento as figuras da configuração inicial e final do potencial foram produzidas utilizando tabelas HTML construídas atribuindo os valores do potencial ao conteúdo das células e um mapa de cinza como cor de fundo das células. Gere uma imagem semelhante utilizando o Plotly (ou sua ferramenta gráfica preferida), como a imagem que segue.
Note que a figura gerada com o Plotly está rodada de 90° no sentido anti-horário com relação à tabela do exercício anterior. Isso ocorre porque no caso da tabela o primeiro índice (i) está referenciando as linhas (eixo $y$) enquanto o segundo índice (j) está referenciando as colunas (eixo $x$). Ao utilizarmos a mesma ordem para construir as matrizes utilizadas como dados para produzir o heatmap com o Plotly, o primeiro índice vai referenciar a coordenada $x$ e o segundo a coordenada $y$. Obviamente podemos compatibilizar as coisas invertendo a ordem dos laços em um dos dois casos, mas aí perderíamos a oportunidade de pensar nisso!
No exemplo a matriz inicial está especificada explicitamente, o que dificulta a implementação de sistemas mais complexos (com uma maior resolução espacial ou muitos potenciais diferentes, por exemplo). Substitua os dados explícitos da matriz cMat por um algoritmo que a preencha segundo algumas regras.
A figura abaixo foi gerada definindo cMat com 41 × 41 elementos, inicialmente "zerados". Isso pode ser feito como segue:

let N = 41; let cMat = []; for (let i=0; i<N; i++) { cMat[i] = []; for (let j=0; j<N; j++) { cMat[i][j] = 0; } }

Em seguida, o perímetro do sistema pode ser ajustado para um valor fixo, como segue (que só funciona para matrizes quadradas):

for (let i=0; i<N; i++) { cMat[i][0] = 1; cMat[i][N-1] = 1; cMat[0][i] = 1; cMat[N-1][i] = 1; }

Feito isso, falta implementar as duas "linhas de carga", que fica como tarefa.
Quanto menor a tolerância especificada, maior o número de interações. O gráfico abaixo mostra o número de interações para tolerâncias de 0,001 V, 0,01 V, 0,1 V, 1 V, 10 V. Modifique o script original de modo a obter o número de interações em cada caso (110, 79, 50, 22, 3), respectivamente) e faça o gráfico utilizando o Plotly ou a ferramenta gráfica de sua preferência.